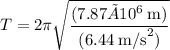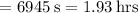Step-by-step explanation:
The artificial satellite experiences a centripetal force
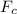 as it moves around the earth and it is defined as
as it moves around the earth and it is defined as
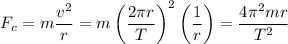
where m is the mass of the satellite, r is its orbital radius and T is its orbital period. But we need to find the radius first.
Recall that the satellite is orbiting at a height where its acceleration due to gravity is 6.44 m/s^2. Since we know that the weight mg of the satellite is equal to the gravitational force
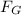 between the earth and the satellite, we can write
between the earth and the satellite, we can write
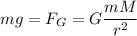
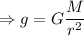
where M is the mass of the earth (=
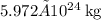 ) and G is the universal gravitational constant (=
) and G is the universal gravitational constant (=
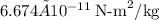 ). Plugging in the values, we find that the radius of the satellite's orbit is
). Plugging in the values, we find that the radius of the satellite's orbit is
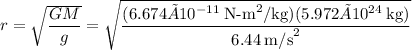
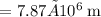
Now that we have the value for the radius, we can now calculate the orbital period T. Recall that the centripetal force is equal to the weight of the satellite at its orbital radius. Therefore,
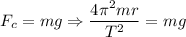
or
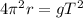
Solving for T, we get
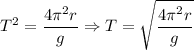
We can further simplify the above expression into
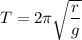
Plugging in the values for r and g, we get