Answer: A. initial value 12, rate of change -2
Explanation:
Find the rate of change and the initial value for the linear relation.
![\left[\begin{array}{ccc}x&y\\1&10\\2&8\\3&6\\4&4\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/9lv2jgvdwm7btxi63saz7s5wamilz33z85.png)
Step 1: Use the two of the points from the table above and solve for the slope = rate of change.
(1, 10) (2, 8)
 =
=
 =
=
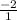 = -2
= -2
Step 2: Using the slope plug it into the slope-intercept form to solve for the initial value or b.
y = mx + b (1, 10)
![\left[\begin{array}{ccc}y=10\\m=-2\\x=1\\b = ?\end{array}\right]](https://img.qammunity.org/2022/formulas/mathematics/college/oumic9uyg8h0ljqxts95dajqxewyt0jn7b.png)
10 = -2(1) + b
10 = -2 + b
+2 +2
12 = b
The initial value of the linear reaction would be 12 and the rate of change is -2.