Question

The width of a triangle is six more than twice the height. The area of the triangle is 88in2. Find the height and width of the triangle.

Answer 1

w = 22 in, h = 8 in.

Explanation:

Reading the problem, I immediately see two equations. This hints me towards a system of equations problem.

Statement 1 is The width of a triangle is six more than twice the height.

The width (w) of a triangle is (=) six (6) more (+) than twice (2) the height (h).

Equation 1: w = 6 + 2h

Statement 2 is The area of the triangle is 88 in2.

The formula for the area of a triangle is
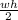`(wh)/(2)`. So, we get our second equation.

Equation 2: wh/2 = 88

We see that we have the same number of equations as unknowns, two. This is important as it lets us know that we can find two unknowns in the two equations. If there are more unknowns than equations, then we cannot find the values of all the variables. Look for another equation in the problem. However, if the # equations greater than or equal to number of unknowns, then we are ready to start solving! So, we can now move to solving.

Equation 1 isolates one of the unknowns (w). So, we can replace w in the second equation with the right side of eq 1. Then, we simplify for h.

`(wh)/(2) = 88`

`((6 + 2h)h)/(2) = 88`

`(6h + 2h^2)/(2) = 88`

`6h + 2h^2 = 176`

`2h^2 + 6h - 176 = 0`

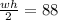
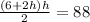
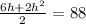
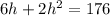
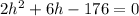
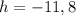`h = -11, 8` (assuming you know how to solve quadratics)

Since we know that heights of triangles cannot be negative, we find that
`h = 8` in.

For the final step, we plug
`h` into our first equation to find
`w`.

`w = 6 + 2h`

`w = 6 + 2(8)`

`w = 6 + 16`

`w = 22`

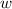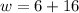
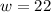
So, the answer is w = 22 in, h = 8 in.

To check if we were right, we can plug the values into both equations to see if they are equal. I will skip equation 1 since we used that equation "as-is" to find w.

`(wh)/(2) = 88`

`(22 * 8)/(2) = 88`

`11 * 8 = 88`

`88 = 88`

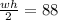
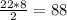
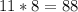
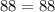
The solution checks out!