Answer:

Explanation:
We are asked to find the equation of the line that passes through the point (2, -1) and has a slope of -3.
We are given a point and the slope, so we can use the point-slope formula.
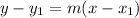
In this formula, m is the slope and (x₁, y₁) is the point the line passes through.
The line has a slope of -3 and passes through (2, -1).
Substitute the values into the formula.
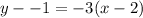
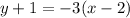
Distribute the -3 on the right side. Multiply each term inside the parentheses by -3.

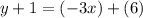
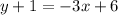
Subtract 1 from both sides of the equation to isolate the variable y.
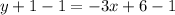
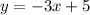
The equation of the line is y= -3x+5.