Answer:
x² + 12x + 36
Explanation:
Given the quadratic expression, x² + 12x + ___, with a missing constant value, c:
We can find the value of the constant by taking the coefficient of the middle term, dividing it by 2, and squaring its quotient. In other words,
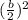 . In the given quadratic expression, b = 12. Substitute the value of b = 12 into
. In the given quadratic expression, b = 12. Substitute the value of b = 12 into
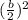 , to find the value of the constant.
, to find the value of the constant.
x² + 12x +
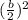
x² + 12x +

x² + 12x + (6)²
x² + 12x + 36 ⇒ This is the perfect square trinomial.
Therefore, the missing value for the constant, c, is 36, making the quadratic equation a perfect square trinomial, x² + 12x + 36.