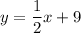Question

(HELP)

Line L has the equation y = -2x - 3.
Line M is perpendicular to Line L and intersects the y-axis at (0,9)
Write Down the equation of Line M in the form y=mx+c

Answer 1

`y=\frac12x+9`

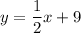
Explanation:

The product of the slopes of perpendicular lines is -1

Given the slope of Line L is -2, this means that the slope of Line M will be:

`(-1)/(-2)=\frac12`

`\sf as \ \frac12 \cdot -2 = -1`

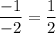
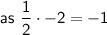
If Line M intersects the y-axis at (0, 9) then its y-intercept is 9.

Slope-intercept of a linear equation:
`y = mx + c`

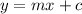
(where m is the slope and c is the y-intercept)

Therefore, the equation for Line M is:

`y=\frac12x+9`