Question

-8-8-6-2 4 12 22
What is the nth term rule of the quadratic sequence

Answer 1

`n^2 -3n - 6`

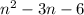
Explanation:

Looking at the image attached, you must first work out the difference between each term. This is +0, +2, +4, +6, +8, +10 (shown in orange).

Because you now have a linear sequence, the difference is now the same each time. This is +2 (shown in blue).

Because the original sequence is a quadratic, you have to halve the second difference (the +2). This means that the value of
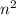`n^2` is 1, so 1
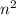`n^2` or just
`n^2` .

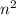If you write out the values of
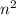`n^2`, you can work out how much more you need to add or take away. For example, take the first three terms in the sequence.

n = 1, 2, 3

x = -8, -8, -6

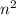`n^2` = 1, 4, 9

Work out the difference between
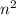`n^2` and x:

1 - -8 = 9

4 - -8 = 12

9 - -6 = 15

This gives you yet another linear sequence, 9, 12, 15.

Working out the formula for this, the difference is 3 each time, so it is 3n. The first value of n is 1, so 3n is 1. The difference is 6, so the formula for this linear sequence is 3n + 6.

Because
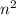`n^2` is greater than x, you need to take 3n + 6 away from
`n^2`.

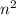This gives
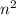`n^2` - (3n+6), so the final answer is:

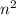`n^2` - 3n - 6.