9514 1404 393
Answer:
10.49
Explanation:
Since we know 110 = 10² +10, we can make a first approximation to the root as ...
√10 ≈ 10 +10/21 . . . . . where 21 = 1 + 2×integer portion of root
This is a little outside the desired approximation accuracy, so we need to refine the estimate. There are a couple of simple ways to do this.
One of the best is to use the Babylonian method: average this value with the value obtained by dividing 110 by it.
((220/21) + (110/(220/21)))/2 = 110/21 +21/4 = 881/84 ≈ 10.49
An approximation of √110 accurate to hundredths is 10.49.
__
The other simple way to refine the root estimate is to carry the continued fraction approximation to one more level.
For n = s² +r, the first approximation is ...
√n = s +r/(2s+1)
An iterated approximation is ...
s + r/(s +(s +r/(2s+1)))
The adds 's' to the approximate root to make the new fraction denominator.
For this root, the refined approximation is ...
√110 ≈ 10 + 10/(10 +(10 +10/21)) = 10 +10/(430/21) = 10 +21/43 ≈ 10.49
_____
Additional comment
Any square root can be represented as a repeating continued fraction.
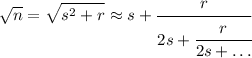
If "f" represents the fractional part of the root, it can be refined by the iteration ...
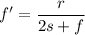
__
The above continued fraction iteration adds 1+ good decimal places to the root with each iteration. The Babylonian method described above doubles the number of good decimal places with each iteration. It very quickly converges to a root limited only by the precision available in your calculator.