Question

PLZ HELPPP ME

Point B has coordinates ​(3​,2​). The​ x-coordinate of point A is 0 . The distance between point A and point B is 5 units. What are the possible coordinates of point​ A?

Answer 1

A (0, - 2 ) or A (0, 6 )

Explanation:

Using the distance formula

d =
`\sqrt{(y_(2)-y_(1))^2+(x_(2)-x_(1))^2 }`

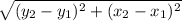
with (x₁, y₁ ) = B(3, 2) and (x₂, y₂ ) = A(0, y )

AB =
`√((0-3)^2+(y-2)^2)`

=
`√((-3)^2+(y-2)^2)`

=
`√(9+(y-2)^2)`

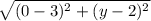
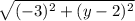
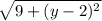
Given AB = 5 then equating gives

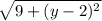`√(9+(y-2)^2)` = 5 ( square both sides )

9 + (y - 2)² = 25 ( subtract 9 from both sides )

(y - 2)² = 16 ( take square root of both sides )

y - 2 = ±
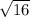`√(16)` = ± 4 ( add 2 to both sides )

y = 2 ± 4

Then y = 2 - 4 = - 2 or y = 2 + 4 = 6

Possible coordinates of point A are

A (0, - 2 ) or A (0, 6 )