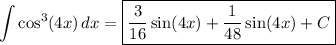Recall the half-angle identity for cosine:
cos²(x) = 1/2 (1 + cos(2x))
Then we can rewrite the integrand as
cos³(4x) = cos(4x) cos²(4x) = 1/2 cos(4x) (1 + cos(8x))
So we have
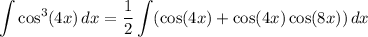
Next, recall the cosine product identity,
cos(a) cos(b) = 1/2 (cos(a - b) + cos(a + b))
so that the integral is equivalent to
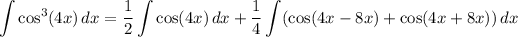
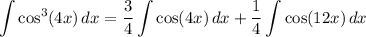
Computing the rest is trivial: