Answer:
y ≤
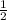 x + 3
x + 3
Explanation:
the equation of the line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
calculate m using the slope formula
m =
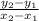
with (x₁, y₁ ) = (- 6, 0) and (x₂, y₂ ) = (0, 3) ← 2 points on the line
m =
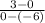 =
=
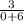 =
=
 =
=
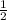
the line crosses the y- axis at (0, 3 ) ⇒ c = 3
y =
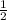 x + 3 ← is the equation of the line
x + 3 ← is the equation of the line
the solution lies below the line and on the line.
as line is solid use ≤
y ≤
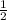 x + 3
x + 3