Question

What is the equation of the line that passes through the point (-3,-6) and (2,-2)

Answer 1

`y=(4)/(5)x-(18)/(5)`

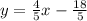
Explanation:

Hi there!

We want to find the equation of the line that passes through the point (-3, -6) and (2, -2)

There are 3 ways to write the equation of the line:

• In slope-intercept form, which is y=mx+b, where m is the slope and b is the y intercept

• In point-slope form, which is
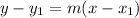  `y-y_1=m(x-x_1)`, where m is the slope and
  `(x_1,y_1)` is a point

• In standard form, which is ax+by=c, where a, b, and c are integer coefficients, but a and b cannot be zero, and a cannot be negative

The easiest way would either be slope-intercept or point-slope form, but let's write the equation in slope-intercept form, since it's the most common way

So we'll need to find the slope

The formula for the slope calculated from 2 points is
`(y_2-y_1)/(x_2-x_1)`, where
`(x_1, y_1)` and
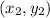`(x_2, y_2)` are points

We have everything needed to find the slope, let's just label the values of the points to avoid any confusion:

`x_1=-3\\y_1=-6\\x_2=2\\y_2=-2`

Now substitute these values into the formula. Remember that m is the value of the slope:

m=
`(y_2-y_1)/(x_2-x_1)`

m=
`(-2--6)/(2--3)`

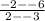
Simplify the fraction:

m=
`(-2+6)/(2+3)`

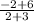
Add the numbers together:

m=
`(4)/(5)`

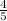
So the slope of the line is 4/5

Let's plug it into the formula y=mx+b, since we now know the value of m

y=
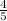`(4)/(5)`x+b

Now let's find b

As the equation passes through both (-3, -6) and (2, -2), we can use either point to help solve for b

Either point works, but let's take (2, -2) for instance

Substitute 2 as x and -2 as y

-2=4/5(2)+b

Multiply

-2=8/5+b

subtract 8/5 from both sides

-18/5=b

Now substitute -18/5 as b into the equation:

`y=(4)/(5)x-(18)/(5)`

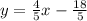
Hope this helps!