Question

Identify the slope and y-intercept of the
equation 2x + 5y = 20

Answer 1

Slope = - ⅖

Y-intercept = (0, 4), where b = 4

Explanation:

Given the linear equation in standard form, 2x + 5y = 20, where A = 2, B = 5, and C = 20:

Start by transforming the standard equation into its slope-intercept form, y = mx + b, where m = slope, and b = y-intercept.

Subtract 2x from both sides:

2x -2x + 5y = - 2x + 20

5y = -2x + 20

Divide both sides by 5 to isolate y:

`(5y)/(5) = (-2x + 20)/(5)`

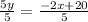
y = - ⅖x + 4 ⇒ This is the slope-intercept form where the slope, m = -⅖, and the y-intercept, b = 4. The y-intercept is the point on the graph where it crosses the y-axis, and has coordinates of (0, b). The y-coordinate is the value of b in the slope-intercept form. Therefore, the y-intercept is (0, 4).