Question

Which is an equation of the parabola that intersects the x-axis at points (-1, 0) and (3, 0)? Show your work or explain how you determined your answer. A. y = x2 + 2x - 3 B. y = x2 + 3x + 2 C. y = x2 - 2x - 3 D. y = x2 - 3x + 2

Answer 1

`\displaystyle \large{y=x^2-2x-3}`

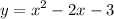
Explanation:

The given points are (-1,0) and (3,0) to find an equation of parabola. Notice that they say or the given points are x-intercepts, which means they make it easier for us to find an equation of parabola using these x-intercepts.

Quick Note:

• x-intercepts are simply the roots or solutions of quadratic equation, so if our root is x = -2 then we can write as (-2,0) and write back to x+2=0.

So what we are going to do is to write the roots’ equation back as
`\displaystyle \large{x+\alpha =0}`

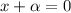
Our points or roots are given, therefore:

If x = -1 then x+1=0

If x = 3 then x-3=0

Then multiply x+1 with x-3 because if (x-1)(x+3)=0 then x-1=0 or x+3=0:

`\displaystyle \large{(x+1)(x-3)=0}`

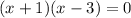
Convert 0 to y since we want to find a function:

`\displaystyle \large{(x+1)(x-3)=y}\\\displaystyle \large{y=(x+1)(x-3)}`

Expand the expressions in and simplify to standard form:

`\displaystyle \large{y=x^2-3x+x-3}\\\displaystyle \large{y=x^2-2x-3}`

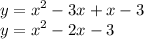
Therefore, the equation is
`\displaystyle \large{y=x^2-2x-3}`

__________________________________________________________

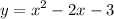
Summary

If we are given the points
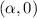`\displaystyle \large{(\alpha ,0)}` and
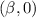`\displaystyle \large{(\beta ,0)}` with wideness of the graph or a-value = 1 then the parabola equation is:

`\displaystyle \large{y=(x-\alpha )(x-\beta )}\\\displaystyle \large{y=x^2-\beta x-\alpha x+\alpha \beta }\\\displaystyle \large{y=x^2-(\beta +\alpha )x+\alpha \beta }`

__________________________________________________________

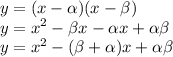
Others

If you have any doubts about my answer, explanation or this question, do not hesitate to let me know in the comment!