Question

What is the slope of (-1,6) and (2,3)?

Answer 1

-1

Explanation:

For a line joining two points (x1, y1) and (x2, y2), it's slope is given as:

`\boxed{ \mathsf{slope = ( y_(2) -y _(1))/( x_(2) - x _(1)) }}`

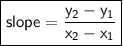
Here, the two points are (-1, 6) and (2, 3) in place of (x1, y1) and (x2, y2).

Solving for slope:

`\implies \mathsf{ (3 - 6)/(2 - ( -1 )) }`

`\implies \mathsf{ ( - 3)/(2 + 1 ) }`

`\implies \mathsf{ ( - 3)/(3 ) }`

`\implies \mathsf{ - 1 }`

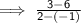
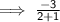
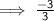
Hence, the slope of the line joining the given points is -1.