Answer:
![\displaystyle y' = - \csc (x) \big[ \cot^2 (x) + \csc^2 (x) \big]](https://img.qammunity.org/2022/formulas/mathematics/high-school/ljfwlnj7i0wio334im4ikbsmtjxbfx2j0v.png)
General Formulas and Concepts:
Algebra I
Terms/Coefficients
Functions
Calculus
Differentiation
- Derivatives
- Derivative Notation
Derivative Rule [Product Rule]:
![\displaystyle (d)/(dx) [f(x)g(x)]=f'(x)g(x) + g'(x)f(x)](https://img.qammunity.org/2022/formulas/mathematics/college/c6fshhoq1mws6w0d0la17c7k2dcytwd8kg.png)
Explanation:
Step 1: Define
Identify.
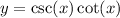
Step 2: Differentiate
- Derivative Rule [Product Rule]:
![\displaystyle y' = (d)/(dx)[\csc (x)] \cot (x) + \csc (x) (d)/(dx)[\cot (x)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/cw6e25z8m88rx7sp5vwg7b1edxc6dmq1qf.png)
- Trigonometric Differentiation:
![\displaystyle y' = - \csc (x) \cot (x) \cot (x) + \csc (x) \big[ - \csc ^2 (x) \big]](https://img.qammunity.org/2022/formulas/mathematics/high-school/8x388komso1m3zll3lvbk2ukcy9ch35rbk.png)
- Simplify:
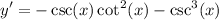
- Factor:
![\displaystyle y' = - \csc (x) \big[ \cot^2 (x) + \csc^2 (x) \big]](https://img.qammunity.org/2022/formulas/mathematics/high-school/ljfwlnj7i0wio334im4ikbsmtjxbfx2j0v.png)
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Differentiation