Answer:
Choice C
Explanation:
We are given the function:
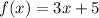
Let
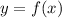 therefore:
therefore:
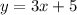
To find an inverse of function, swap the position of x and y:

Then solve or simplify the equation in term of y:
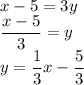
Therefore, the answer is choice C.
__________________________________________________________
Summary
An inverse function is a function that swaps the position of domain and range, defined as notation
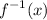 or
or
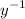 generally. When finding an inverse function, make sure to swap position of range and domain, if given the interval.
generally. When finding an inverse function, make sure to swap position of range and domain, if given the interval.
Only one-to-one functions may have an inverse — multiple-to-one can not have an inverse such as quadratic function or any even-degree polynomial functions.
__________________________________________________________
Others
If you’re still curious or stuck in this question or have any doubts regarding my explanation, answer or this question — always let me know through comments!