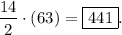Question

Find the sum: -1 + 4 + 9 + ... + 64

Answer 1

= 78

Explanation:

Step One:

1 + 4= 5

Step Two:

5+9= 14

Step Three:

14+64= 78

= 78

Hope it helps :)

Answer 2

Answer: 441

Explanation:

The formula for an arithmetic sum is

`$\frac{\text{number of terms}}2 \cdot (\text{first term + last term})$`

We know that the
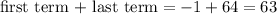`\text{first term + last term} = -1 + 64 = 63`. So now all we need is the
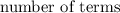`\text{number of terms}`. Well, if you draw each number onto the number line, you get something like

---|------|------|------|------|------|-----|------|-----|------|-----|------|-------|----------

-1 0 1 2 3 4 5 6 7 8 9 10 11 ...

You can see that your numbers are spaced 5 apart, and they go from -1 all the way up to 64. So what you're really asking is, "how many segments of five can I draw from -1 up to 64?" The length of the line from -1 to 64 is 65 (think about it), so the number of line segments is 65/5 = 13. However, we didn't count 64 itself, since there's no line segment past it! So really there are 14 terms in this sequence. Thus the total sum is

`$\frac {14}2 \cdot (63) = \boxed{441}.$`