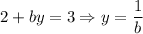49.
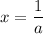 and
and
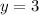
50.
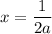 and
and
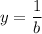
Explanation:
We are going to solve these systems of equations using the elimination method.
49. Given:
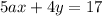 (1)
(1)
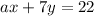 (2)
(2)
Multiply Eqn(1) by 7 and multiply Eqn(2) by -4 to get
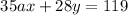
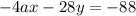
Adding the two equations above, we get
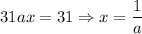
Substituting this value for a into Eqn(2), we get
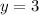
50. Given:
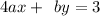 (3)
(3)
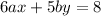 (4)
(4)
Multiplying Eqn(3) by -5, we get
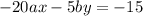
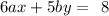
Adding the two equations above, we get
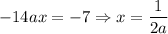
Plugging in the value of x into Eqn(3), we get the value for y as
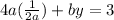
or