9514 1404 393
Answer:
(x, y) = (1.25, 8.5)
Explanation:
I choose to put these equations into reduced general form, then use the "cross multiplication method" to solve.
2x -y +6 = 0
10x -y -4 = 0
d1 = 2(-1) -10(-1) = 8
d2 = -1(-4) -(-1)(6) = 10
d3 = 6(10) -(-4)(2) = 68
Solutions are ...
x = d2/d1 = 10/8 = 1.25
y = d3/d1 = 68/8 = 8.5
The solution is (x, y) = (1.25, 8.5).
_____
Additional comment
I like a graphing calculator for a quick and easy solution. When the values are not integers, I like an algebraic solution to see what the exact values are.
__
The "cross multiplication method" is similar to Cramer's rule in that determinants of pairs of coefficients are computed. If you look up this method, videos will show you a variation that is slightly different. Here, we determined d1, d2, and d3 as the 2×2 determinant of the coefficients in adjacent columns of the array you get from the general form equations with the first column repeated:
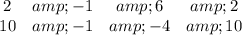
In each pair, the determinant is the difference between the product of numbers on the down-diagonal and the product of numbers on the up-diagonal.
The determinants relate to the x- and y-values by ...
1/d1 = x/d2 = y/d3 ⇒ x = d2/d1, y = d3/d1
There is a Vedic solution method for linear equations that is similar to this, but starts from equations in standard form. As a consequence, the cross-differences are done in a different order.
__
Standard form: ax +by = c
General form: ax +by +c = 0