Question

`\displaystyle \sf\lim_(x \to 0 ) \frac{1 - \prod \limits_(k = 2)^(n) \sqrt[k]{cos(kx)} }{ {x}^(2) } = 10`

​

Answer 1

`\displaystyle \rm\lim_(x \to 0 ) \frac{1 - \prod \limits_(k = 2)^(n) \sqrt[k]{cos(kx)} }{ {x}^(2) } = 10`

`\displaystyle\rm Let \: y = \prod_(k = 2)^n \sqrt[k]{cos (kx)}`

`\to \rm logy = log \prod \limits _(k = 1)^(n) \sqrt[k]{cos(kx)}`

`{ \to\rm logy = \sum \limits_(k = 2)^(n) log( \sqrt[k]{ \cos(kx) } ) = \sum \limits_(k = 2)^(n) (1)/(k) \log( \cos(kx) ) }`

`\rm differentiate \: wrtx`

`{\displaystyle \to \rm (1)/(y) \: dy = \sum_(k = 2)^( n ) \bigg\{ \frac{1}{ \cancel{k}} \cdot(1)/( \cos(kx) ) \cdot - \cancel{k} \sin(kx) \bigg \}}`

`\displaystyle \to \rm dy = - y \sum_(k = 2)^(n) \tan(kx)`

`\rm{Now}`

`\displaystyle \rm \lim_(x \to0) \frac{1 - y}{ {x}^(2) } = ( - dy)/(2x) \: \: \: \: [using - Hopitals \: rule ]`

`\displaystyle \rm = \lim_(x \to0) \frac{y}{ {2} } \sum_(k = 2)^(n) ( \tan(kx) )/(kx) * k`

`\displaystyle \rm = \lim_(x \to0) \frac{y}{ {2} } \sum_(k = 2)^(n) k \: \: \: \: \: \bigg [note \: \displaystyle \rm\lim_(x \to0) \: y = 1 \bigg]`

`\rm= (1)/(2) \bigg [ (n(n + 1))/(2) - 1\bigg] = 10`

`\rm \to n(n + 1) = 2(20 + 1) = 42 = 6 * 7 = 6(6 + 1)`

`\rm \boxed{ \rm{n = 6}}`

Answer 2

To demonstrate a method for computing the limit itself, let's pick a small value of n. If n = 3, then our limit is

`\displaystyle \lim_(x \to 0 ) \frac{1 - \prod \limits_(k = 2)^(3) \sqrt[k]{\cos(kx)} }{ {x}^(2) }`

Let a = 1 and b the cosine product, and write them as

`(a - b)/(x^2)`

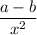
with

`b = √(\cos(2x)) \sqrt[3]{\cos(3x)} = \sqrt[6]{\cos^3(2x)} \sqrt[6]{\cos^2(3x)} = \left(\cos^3(2x) \cos^2(3x)\right)^(\frac16)`

Now we use the identity

`a^n-b^n = (a-b)\left(a^(n-1)+a^(n-2)b+a^(n-3)b^2+\cdots a^2b^(n-3)+ab^(n-2)+b^(n-1)\right)`

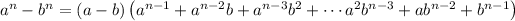
to rationalize the numerator. This gives

`\displaystyle (a^6-b^6)/(x^2 \left(a^5+a^4b+a^3b^2+a^2b^3+ab^4+b^5\right))`

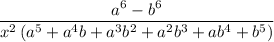
As x approaches 0, both a and b approach 1, so the polynomial in a and b in the denominator approaches 6, and our original limit reduces to

`\displaystyle \frac16 \lim_(x\to0) (1-\cos^3(2x)\cos^2(3x))/(x^2)`

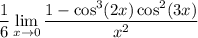
For the remaining limit, use the Taylor expansion for cos(x) :

`\cos(x) = 1 - \frac{x^2}2 + \mathcal{O}(x^4)`

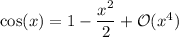
where
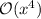`\mathcal{O}(x^4)` essentially means that all the other terms in the expansion grow as quickly as or faster than x⁴; in other words, the expansion behaves asymptotically like x⁴. As x approaches 0, all these terms go to 0 as well.

Then

`\displaystyle \cos^3(2x) \cos^2(3x) = \left(1 - 2x^2\right)^3 \left(1 - \frac{9x^2}2\right)^2`

`\displaystyle \cos^3(2x) \cos^2(3x) = \left(1 - 6x^2 + 12x^4 - 8x^6\right) \left(1 - 9x^2 + \frac{81x^4}4\right)`

`\displaystyle \cos^3(2x) \cos^2(3x) = 1 - 15x^2 + \mathcal{O}(x^4)`

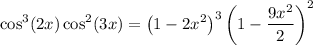
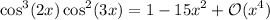
so in our limit, the constant terms cancel, and the asymptotic terms go to 0, and we end up with

`\displaystyle \frac16 \lim_(x\to0) (15x^2)/(x^2) = \frac{15}6 = \frac52`

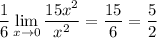
Unfortunately, this doesn't agree with the limit we want, so n ≠ 3. But you can try applying this method for larger n, or computing a more general result.

Edit: some scratch work suggests the limit is 10 for n = 6.