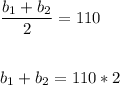Answer:
Explanation:
17) In parallelogram, adjacent angles are supplementary (add up to 180)
⇒∠A + ∠D = 180
5x + 30 + x = 180
5x +x + 30 = 180 {Combine like terms}
6x + 30 = 180 {Now, subtract 30 from both sides}
6x + 30 - 30 = 180 - 30
6x = 150
Now divide both sides by 6
x = 150/6
x = 25
∠A = 5x + 30
= 5*25 + 30
= 125 + 30
= 155
In parallelogram, opposite angles are congruent.
∠C = ∠A
∠C = 155°
18)In parallelogram, adjacent angles are supplementary (add up to 180)
⇒∠A + ∠D = 180
3x + 4 + x = 180
3x +x + 4 = 180 {Combine like terms}
4x + 4 = 180 {Now, subtract 4 from both sides}
4x + 4 - 4 = 180 - 4
4x = 176
Now divide both sides by 4
x = 176/4
x =44
19) In parallelogram, adjacent angles are supplementary (add up to 180)
⇒∠GAC + ∠ACF = 180
125 + ∠ACF = 180
Now, subtract 125 from both sides
∠ACF = 180 - 125
∠ACF = 55
21) In parallelogram, adjacent angles are supplementary (add up to 180)
∠CFG + ∠ACF = 180
2w +30 + w + 15 = 180
2w +w + 30+ 15 = 180
3w + 45 = 180
3w = 180 - 45
3w = 135
w = 135/3
w = 45
∠ACF = w + 15
= 45 + 15
∠ACF = 60
21) In parallelogram, opposite sides are congruent.
GF = AC
4x - 14 = 2x + 2
4x = 2x + 2 + 14
4x = 2x + 16
4x - 2x = 16
2x = 16
x = 16/2
x = 8
22) In parallelogram, the diagonals bisect each other.
XC = GX
3y - 3 =2y + 2
3y = 2y + 2 + 3
3y = 2y + 5
3y - 2y= 5
y = 5
23) The length of the middle segment of trapezium is half the sum of the two parallel sides.