Answer:
y = 116°
Explanation:
Given that L₁ || L₂:
The exterior angle theorem states that the measure of an exterior angle of a triangle is equal to the sum of the two opposite and non-adjacent remote interior angles.
Also, ∠y° and ∠2x° are same-side interior angles formed by the intersection of the hypotenuse of the triangle that acts as a transversal to the parallel lines, L₁ and L₂. Given that ∠y° and ∠2x° are same-side interior angles, then it means that they are the supplements of each other, such that the sum of their measures is 180°.
Now that we have established these definitions, we can proceed with the solution.
Equation 1: ∠y° + ∠2x° = 180° ⇒ Same-side interior angles
Equation 2: ∠y° = ∠x° + ∠84° ⇒ exterior angle theorem
Substitute the value of m∠y° from Equation 2 into Equation 1 to solve for the value of x:
∠y° + ∠2x° = 180°
∠x° + ∠84° + 2x° = 180°
Combine like terms:
∠3x° + ∠84° = 180°
Subtract ∠84° from both sides:
∠3x° + ∠84° - ∠84° = 180° -∠84°
∠3x° = 180° - ∠84°
∠3x° = 96°
Divide both sides by 3 to solve for x:
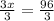
∠x° = 32°
Substitute the value of x into Equation 2 to solve for y:
∠y° = ∠x° + ∠84°
∠y° = ∠32° + ∠84°
∠y° = 116°
Verify whether the values for x and y are correct by substituting their values into Equation 1 and 2:
Equation 1:
∠y° + ∠2x° = 180°
116° + 2(32)° = 180°
116° + 64° = 180°
180° = 180° (True statement).
Equation 2:
∠y° = ∠x° + ∠84°
116° = 32° + 84°
116° = 116° (True statement)
Therefore, the correct answer is: y = 116°.