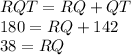Answer:
The following measurements are:
 (Option #4)
(Option #4)
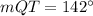 (Option #7)
(Option #7)
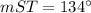 (Option #5)
(Option #5)
 (Option #2)
(Option #2)
Explanation:
To begin, we can find the measure of
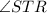 by applying the inscribed angle theorem: an angle θ inscribed in a circle is half of the central angle 2θ that subtends the same arc on the circle.
by applying the inscribed angle theorem: an angle θ inscribed in a circle is half of the central angle 2θ that subtends the same arc on the circle.
Since the intercepted arc (RS) is 46 degrees, we have:
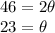
Next, we can find the measure of arc QT using the same theorem. So,
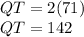
Notice that the chord RT is actually a diameter. From the theorem about the inscribed angle including a diameter, we know that the intercepted arc will have a measure of
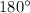 . Since the arc ST is part of the arc RST, and we know RS is
. Since the arc ST is part of the arc RST, and we know RS is
 , we can set up and solve this equation:
, we can set up and solve this equation:

We can use the same idea to find RQ. We know that RQT is
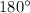 and QT is
and QT is
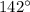 , so:
, so: