Recall the binomial theorem:
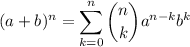
a. Let a = b = 1 and n = 8. Then the sum above gives the sum shown here,
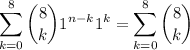
so it reduces to (1 + 1)⁸ = 2⁸ = 256.
b. Let a = 1 and b = -1 and k = 8. Then by the same argument, the sum reduces to (1 - 1)⁸ = 0.
c. Notice that
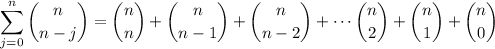
but this is nearly identical to the sum in part a, with a = b = 1 and arbitrary n, but the order of terms is reversed. Then it reduces to (1 + 1)ⁿ = 2ⁿ.
d. Let a = 1 and b = 2. Then the sum is (1 + 2)ⁿ = 3ⁿ.