a. This is just shifting the index of summation:

and just swap j with k, since you can freely use any symbol for the index.
That is, the identity relies on simple integer arithmetic: 0 + 1 = 1 = 2 - 1, and 1 + 1 = 2 = 3 - 1, and so on.
b. This is something of a generalization of the identity in part a.
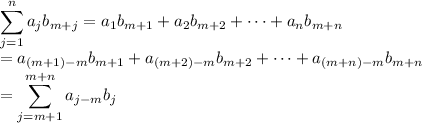
c. Distribute the summation to get

The second sum here is just adding together m copies of 1,
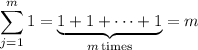
so
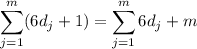
d. The sum as given is generally not true:
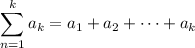
while (generalizing the identity from part c)
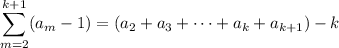
and these expressions are equal only if
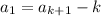 .
.