Answer:
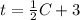
Explanation:
Let's first write the data you have in an equation form:
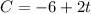 . When t = 0, at dawn, you get -6°C so we're good. But you've ben asked the inverse relationship, so let's solve for t instead.
. When t = 0, at dawn, you get -6°C so we're good. But you've ben asked the inverse relationship, so let's solve for t instead.

Last two are both viable solution, only difference is in form. I do prefer the last option since it makes it easiest at a glance to answer to the question "at what time there's a temperature of 0°C?"