Answer:
x = -5/3, y = -1 or

Explanation:
Solving systems of linear equations using process of elimination involves eliminating one of the variables (and its coefficient) in order to solve the other variable either through addition or subtraction. However, there may be other mathematical operations necessary before one of the variables can be eliminated.
Equation 1: 3y - 6x = 7
Equation 2: -4y - 3x = 9
Step 1: Multiply Equation 2 by -2:
(-2)(-4y - 3x) = 9 (-2)
8y + 6x = -18
Step 2: Add "8y + 6x = -18" to Equation 1:
8y + 6x = -18
+ 3y - 6x = 7
11y = -11
Step 3: Divide both sides by 11 to solve for y:
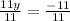
y = -1
Step 4: Substitute y = -1 into Equation 2 to solve for x:
-4(-1) - 3x = 9
4 - 3x = 9
Step 5: Subtract 4 from both sides:
4 - 4 - 3x = 9 - 4
- 3x = 5
Step 6: Divide both sides by -3 to solve for x:
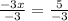
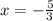
Verify whether the values for x and y are correct by substituting their values into both equations:
x = -5/3, y = -1
Equation 1: 3y - 6x = 7
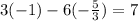
-3 + 10 = 7
7 = 7 (True statement).
Equation 2: -4y - 3x = 9
-4(-1) - 3 (-5/3) = 9
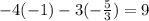
4 + 5 = 9
9 = 9 (True statement).
Therefore, x = -5/3 and y = -1 are the solutions to the given systems of linear equations.