Answer:
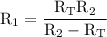
Explanation:
Just an alternative.
we would like to solve the following equation for
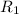 .
.
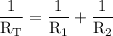
in order to do so,we can simplify the right hand side which yields:
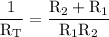
Steps, used to simplify the right hand side:
- find the LCM of the denominators of the fractions i.e LCM(R_1,R_2)=R_1•R_2
- divide the LCM by the denominator of every fraction
- multiply the result of the division by the numerator of every fraction
Cross multiplication:
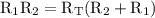
distribute:
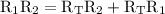
isolate
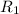 to the left hand side and change its sign:
to the left hand side and change its sign:
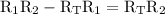
factor out
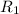 from the left hand side expression:
from the left hand side expression:
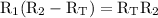
divide both sides by
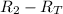 :
:
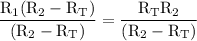
reduce fraction:
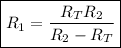
and we're done!