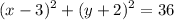Question

Write an equation of the circle with center (3,-2) and radius 6

Answer 1

`\displaystyle (x-3)^2 + (y+2)^2 = 36`

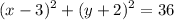
Explanation:

We want to write the equation of a circle with a center at (3, -2) and a radius of 6 units.

Recall that the equation of a circle is given by:

`\displaystyle (x-h)^2 + (y-k)^2 = r^2`

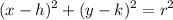
Where (h, k) is the center and r is the radius.

Since our center is at (3, -2), h = 3 and k = -2. r = 6. Substitute:

`\displaystyle (x-(3))^2 +(y-(-2))^2 = (6)^2`

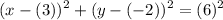
Simplify:

`\displaystyle (x-3)^2 + (y+2)^2 = 36`

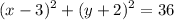
In conclusion, the equation of the circle will be:

`\displaystyle (x-3)^2 + (y+2)^2 = 36`