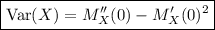Question

A continuous random variable X has probability density function X. Show how its

moment generating function can be used to determine the variance of this random
variable.

Answer 1

The moment generating function is defined by

`M_X(t) = \mathbb E[e^(tX)]`

Recall the power series expansion for the exponential function:

`\displaystyle \sum_(n=0)^\infty (x^n)/(n!) = 1 + x + \frac{x^2}2 + \frac{x^3}6 + \cdots`

Then by extension, the MGF could be similarly written as

`\displaystyle M_X(t) = \mathbb E \left[1 + Xt + \frac{(Xt)^2}2 + \frac{(Xt)^3}6 + \cdots\right]`

There's a certain theorem (due to Fubini, in case you're interested in learning more about it) that let's us exchange the order of integration (recall the definition of expectation for continuous random variables) and summation, so that

`\displaystyle M_X(t) = \mathbb E[1] + \mathbb E[Xt] + \mathbb E\left[\frac{X^2t^2}2\right] + \mathbb E\left[\frac{X^3t^3}6\right] + \cdots`

and by the linearity of expectation,

`\displaystyle M_X(t) = 1 + \mathbb E[X] t + \frac12 \mathbb E\left[X^2\right] t^2 + \frac16 \mathbb E\left[X^3\right] t^3 + \cdots`

and here we see where the name MGF comes from: the coefficient of the n-th order term in the series expansion "generates" the n-th moment, which is defined as E[Xⁿ].

Now, recall the definition of variance:

`\mathrm{Var}(X) = \mathbb E\left[\left(X - \mathbb E[X]\right)^2\right]`

`\mathrm{Var}(X) = \mathbb E\left[X^2\right] - \mathbb E[X]^2`

and this is exactly the difference between the second moment and the square of the first moment.

So if you know the MGF, then you essentially get the variance for free with little effort. By differentiating the MGF, we get

`\displaystyle M_X''(t) = \mathbb E[X] + \mathbb E\left[X^2\right] t + \frac12 \mathbb E\left[X^3\right] t^2 + \cdots`

and setting t = 0 lets us recover the first moment, E[X].

Differentiating again gives

`\displaystyle M_X'(t) = \mathbb E\left[X^2\right] + \mathbb E\left[X^3\right] t + \cdots`

and setting t = 0 once again recovers the second moment.

Then in terms of the MGF, we have

`\boxed{\mathrm{Var}(X) = M_X''(0) - M_X'(0)^2}`