Answer:
y = 2(x - 3)² - 2
Explanation:
Given the quadratic equation with a y-intercept of (0, 16), and has a vertex occurring at point (3, -2):
We can substitute these values into the following vertex form of the quadratic equation:
y = a(x - h)² + k
where:
(h, k) = vertex
a = determines the wideness or narrowness of the graph, and the direction of where the parabola opens.
- a > 1: the graph is narrower than the parent function; the parabola also opens upward.
- 0 < a < 1: the graph is wider than the parent function.
- a < 1: the graph opens downward.
Now that we established the definitions for the variables in the vertex form, we can finally substitute the vertex, (3, -2) and y-intercept, (0, 16) into the vertex form and solve for the value of a:
y = a(x - h)² + k
16 = a(0 - 3)² - 2
16 = a(-3)² - 2
16 = 9a - 2
Add 2 to both sides:
16 + 2 = 9a - 2 + 2
18 = 9a
Divide both sides by 9 to solve for a:
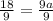
2 = a
Therefore, the quadratic equation in vertex form is:
y = 2(x - 3)² - 2
Attached is a screenshot of the graphed equation, where it shows the y-intercept and the vertex.