Answer:
 .
.
Explanation:
The leading term of a one-variable polynomial refers to the term with the highest power of the variable. For example, in the polynomial
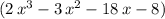 ,
,
 is the variable, and
is the variable, and
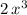 is the leading term. The power of the leading term
is the leading term. The power of the leading term
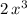 is
is
 .
.
The numerator is
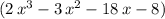 while the denominator is
while the denominator is
 .
.
- Leading term of the numerator:
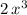 .
. - Leading term of the denominator:
 .
.
Divide the leading term of the numerator by the leading term of the denominator to find the next term of the quotient. In this case,
 .
.
Multiply the denominator by the quotient that was just found. In this case,
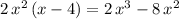 . Subtract this product from the current numerator to find the next numerator:
. Subtract this product from the current numerator to find the next numerator:
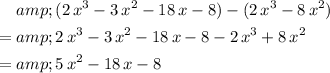 .
.
Thus, the next numerator would be
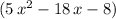 . The denominator stays
. The denominator stays
the same.
Repeat the steps above until the power of the numerator is less than that of the denominator.
The numerator is
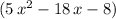 while the denominator is still
while the denominator is still
 .
.
- Leading term of the numerator:
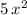 .
. - Leading term of the denominator:
 .
.
Next term of the quotient:
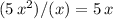 . Add that term to the quotient. The quotient is now
. Add that term to the quotient. The quotient is now
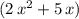 .
.
The next numerator should be:
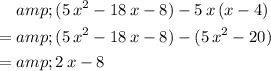 .
.
The numerator is now
 while the denominator continues to be the same.
while the denominator continues to be the same.
- Leading term of the numerator:
 .
. - Leading term of the denominator:
 .
.
Next term of the quotient:
 . Add that term to the quotient to get
. Add that term to the quotient to get
 .
.
The next numerator should be:
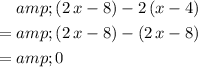 .
.
The numerator is now a constant. The power of
 is the current numerator would be
is the current numerator would be
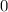 . The power of
. The power of
 in the denominator continues to be
in the denominator continues to be
 . Thus, the power of the numerator is now less than that of the denominator.
. Thus, the power of the numerator is now less than that of the denominator.
The quotient is now the required quotient, with the "numerator" being the remainder of the division. That is:
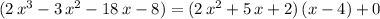 .
.
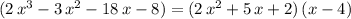 .
.
Equivalently:
 .
.