Question

Find the coefficient of x of (1+2/x²) (2x-3/x)⁵

Answer 1

First, we have

(1 + 2/x²) (2x - 3/x)⁵ = (2x - 3/x)⁵ + 2/x² (2x - 3/x)⁵

In the expansion of (2x - 3/x)⁵, there is no x² term. Each term takes the form

`c (2x)^(5 - i) \left(-\frac3x\right)^i`

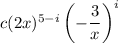
where c is a binomial coefficient, and i is taken from the range {0, 1, 2, 3, 4, 5}. Looking at just the power of x in the product, we have

`x^(5 - i) \left(\frac1x\right)^i = x^(5 - 2i)`

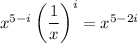
and 5 - 2i = 1 only if i = 2. By the binomial theorem, this term is given by

`\dbinom52 (2x)^(5-2) \left(-\frac3x\right)^2 = (5!)/(2!(5-2)!) \cdot 2^3 \cdot (-3)^2 x = 720x`

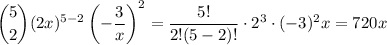
In the other expansion, we have an additional factor of 1/x², so that any given them in the expansion contains a power of x of the form

`\frac1{x^2} x^(5 - i) \left(\frac1x\right)^i = x^(3 - 2i)`

and 3 - 2i = 1 only if x = 1. This term in the expansion is

`\frac2{x^2} \dbinom51 (2x)^(5-1) \left(-\frac3x\right)^1 = (5!)/(1!(5-1)!) \cdot 2^5 \cdot (-3)^1 x = -480x`

Then the coefficient of the x term in the whole expansion is 720 - 480 = 240.