Question

Solve the system of equations by the substitution method.

3x + 2y=22
x=5y-4
Type an ordered pair

Answer 1

(6,2)

Explanation:

To solve this equation using the substitution method we can plug in the given value of x into the equation, 3x+2y=22 and solve for y. Once we get the value of "y" then we can plug the y into our second equation which is x=5y-4.

3x+2y=22

plug in 5y-4 for the x value, so

3(5y-4)+2y=22 now distribute the 3 to the (5y-4) (multiply the 3 by 5y and -4)

3*5y= 15y and 3*-4= -12,

15y-12+2y=22 ←this is our equation after distributing

we can combine the 15y and 2y because they share the same variable

(15y+2y)

17y-12=22 add 12 to both sides to eliminate the -12 and divide by 17 to get rid of the 17 next to y or isolate the y variable

17y-12+12=22+12 → 17y=34 divide both sides by 17

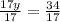`(17y)/(17) =(34)/(17)` the 17's cancel and the 17 divides into 34, leaving us with

y=2

now substitute the y=2 into the equation x=5y-4

so x=5(2)-4 → x=10-4 → x=6

So we have the values for both our x and y values, all we need to do is put them in an ordered pair in the form (x,y)

so the ordered pair is (6,2)