The left side is equivalent to
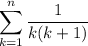
When n = 1, we have on the left side
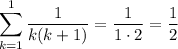
and on the right side,
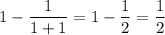
so this case holds.
Assume the equality holds for n = N, so that
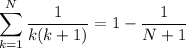
We want to use this to establish equality for n = N + 1, so that
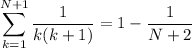
We have
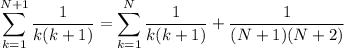
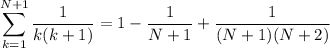
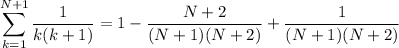
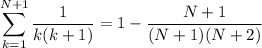
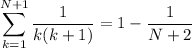
and this proves the claim.