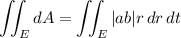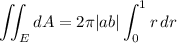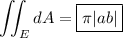An ellipse has the general equation
(x/a)² + (y/b)² = 1
(actually, this is an ellipse whose semimajor and -minor axes are parallel to the x- and y-axes, but one can rotate any ellipse so that it has the same configuration, and the area remains constant)
Convert to a kind of rescaled polar coordinates, using
x = a r cos(t)
y = b r sin(t)
Then the interior of such an ellipse is the set
E = {(r, t) : 0 ≤ r ≤ 1 and 0 ≤ t ≤ 2π}
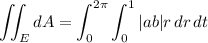
The area of E is then given by the integral
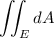
Compute the Jacobian determinant for this change of coordinates. The Jacobian is
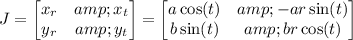
Then we have Jacobian determinant
|det(J)| = |a b r cos²(t) + a b r sin²(t)| = |a b r| = |a b| r
since r ≥ 0.
The area of E is then