Hello there.
First, assume the numbers
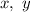 such that they satisties both affirmations:
such that they satisties both affirmations:
- The sum of the squares of two numbers is
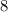 .
. - The product of the two numbers is
 .
.
With these informations, we can set the following equations:

Multiply both sides of the second equation by a factor of
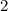 :
:

Make
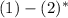
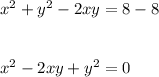
We can rewrite the expression on the left hand side using the binomial expansion in reverse:
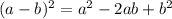 , such that:
, such that:

The square of a number is equal to
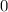 if and only if such number is equal to
if and only if such number is equal to
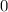 , thus:
, thus:
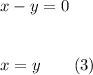
Substituting that information from
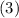 in
in
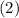 , we get:
, we get:
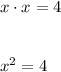
Calculate the square root on both sides of the equation:
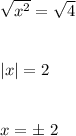
Once again with the information in
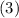 , we have that:
, we have that:
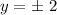
The set of solutions of that satisfies both affirmations is:

This is the set we were looking for.