Answer:
1. First, we need to find the area of the rectangle, then subtract the non-shaded region from the total of the rectangle's area.
Area of rectangle formula;
A = LW
Where 'L' represents the length, and 'W' represents the width.
Plug in your values:
A = LW
A = 8(13)
A = 104, now that we've found the area of this total rectangle, we need to find the area of the triangle and subtract that from the area of the rectangle.
Formula for area of triangle;
A = BH x 1/2
Where 'B' represents the base, and 'H' represents the height and 1/2 is just 1/2.
But, if we look at this triangle we can see that we don't have the base.
So what we have to do is subtract the given side lengths beside it (which you add up) from the total width.
Given length beside unknown base: 4 and 4
So, (4 + 4) = 8, and the total width is 13.
So: 13 - 8 = 5, 5 is our base.
Now we plug these into our formula:
A = BH x 1/2
A = 5(6) x 1/2
A = 30 x 1/2
A = 30/2, which equals to 15.
Now we subtract the non shaded region(triangle) from the shaded region(total area of rectangle).
104 - 15 = 89 meters.
2. In this figure, we find the area of the whole triangle, not considering the small empty vertical-positioned rectangle to the bottom left corner.
Let's find the total base and total height.
As we can see, in the bottom triangle the height is 4, the other triangle has a height of 5. Combine these to get (4 + 5) = 9 is our total height of the whole triangle.
Now we find the base, 5 is the base of the bottom triangle and the other triangle has a base of 2, combine these to get: (5 + 2) = 7 is the total base of the whole triangle.
Now plug these into our formula of area of triangle;
A = BH x 1/2
A= 7(9) x 1/2
A = 63/2
A = 31.5, is the area of the whole triangle.
Now let's find the area of the empty rectangle to our bottom left corner.
Our length is 4, our width is 2.
A = LW
A = 4(2)
A = 8
Now subtract the empty rectangle's area from the total area of the triangle:-
31.5 - 8 = 23.5 inches.
3. We can see that in this figure, there is an empty semi circle(that has no area) apart of a square.
So to find the area of the unfinished square, we find the area of the semi circle and subtract it from the total area of the square.
Formula for area of a circle:
A = π
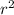
Where 'π' represents pi aka (22/7 or 3.14), and 'r' represents the radius which is being squared.
But if we were to find the area of a semi circle, we would have to divide the whole formula of a regular circle by 2.
So, A = π
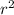 /2
/2
Now, we plug in the values showing in the diagram into our equation.
Though, since we are given a diameter of 6, we need to find the radius which is 1/2(half) of the diameter.
SO,
1/2 x 6 = 3.
Now that we have our radius, we can finally plug this into our equation:-
A = π
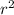 /2
/2
A = 3.14(3^2)/2
A = 3.14(9)/2
A = 28.26/2
A = 14.13, is our area of the semi circle.
Now we have to find the total area of the square, which we easily just multiply the two lengths.
6(length) x 6(width)
= 36, is the area of the total square.
Now we subtract the area of the semi circle from the area of the total square:
36 - 14.13 = 21.87 feet.
4. To find the area of this, we must split the figure into two shapes, a rectangle and a semi circle.
Using the formulas we applied to our past problems;
(Rectangle)
A = LW
A = 20(8)
A = 160, is the area of the rectangle
Now the semi circle (ignore the 12.56, because it's just the circumference):
We have to find the radius, (1/2 x diameter), so: (1/2 x 8) = 4 is our radius.
A = π
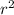 /2
/2
A = 3.14(4^2)/2
A = 3.14(16)/2
A = 50.24/2
A = 25.12, is the area of the semi circle.
Now we add the two areas,
160 + 25.12 = 185.12 feet.
5. We split this figure into two shapes, a rectangle and a triangle.
Using the formulas we applied earlier to our past problems.
(Rectangle)
A = LW
A = 14(12)
A = 168, is the area of the rectangle.
(Triangle)
A = BH x 1/2
A = 8(12) x 1/2
A = 96 x 1/2
A = 96/2
A = 48, is the area of the triangle.
Now we add these areas;
168 + 48 = 216 centimetres.