Question

Use the definition of the derivative to differentiate f(x)= In x

Answer 1

By def. of the derivative, we have for y = ln(x),

`\displaystyle (dy)/(dx) = \lim_(h\to0) (\ln(x+h)-\ln(x))/(h)`

`\displaystyle (dy)/(dx) = \lim_(h\to0) \frac1h \ln\left((x+h)/(x)\right)`

`\displaystyle (dy)/(dx) = \lim_(h\to0) \ln\left(1+\frac hx\right)^(\frac1h)`

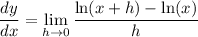
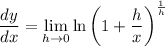
Substitute y = h/x, so that as h approaches 0, so does y. We then rewrite the limit as

`\displaystyle (dy)/(dx) = \lim_(y\to0) \ln\left(1+y\right)^{\frac1{xy}}`

`\displaystyle (dy)/(dx) = \frac1x \lim_(y\to0) \ln\left(1+y\right)^(\frac1y)`

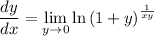
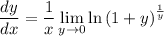
Recall that the constant e is defined by the limit,

`\displaystyle e = \lim_(y\to0) \left(1+y\right)^(\frac1y)`

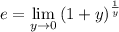
Then in our limit, we end up with

`\displaystyle (dy)/(dx) = \frac1x \ln(e) = \boxed{\frac1x}`

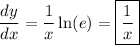
In Mathematica, use

D[Log[x], x]