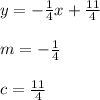Question

Heya!

- If the line y = mx + c passes through the point of intersection of the lines x - 2y = -1 and y = 2 and is perpendicular to the line y = 4x + 8 , then find the values of m and c.

Help!! Irrelevant / Random answers will be reported*​

Answer 1

Hey There!

Let's solve...

We know that the given line is

`y = 4x + 8 \\`

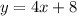
Slope is

`m_(g) = 4 \\`

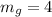
The answer is perpendicular to m which is the negative reciprocal of m_g

`m = - (1)/( m_(g) ) = - (1)/(4) \\`

`y = 2 \\ x = 2(2) = - 1 \\ x = 4 - 1 = 3 \\ x = 3`

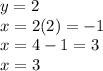
The intersection point is

(3,2)

If we substitute the point into

`y = mx + c \\ y = - (1)/(4)x + c \\`

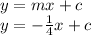
Now let's solve y intercept...

`2 = - (1)/(4)(3) + c \\ \\ c = 2 + (3)/(4) \\`

`= (8)/(4) + (3)/(4) \\ \\ = (8 + 3)/(4) = (11)/(4)`

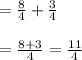
Now the required lines are

`y = - (1)/(4)x + (11)/(4) \\ \\ m = - (1)/(4) \\ \\ c = (11)/(4)`