Hello studentUnion!
Solve the equation-
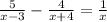
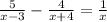
Let's multiply both the sides of the equation by x (x - 3) & (x + 4) which is the LCM of (x - 3), (x + 4) & x. We can't solve it directly without taking the LCM first as the denominators are not equal to each other. Then do cross multiplication. After all these steps, you'll get an equation as..
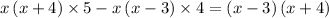
Now, use the distributive property & simplify it.
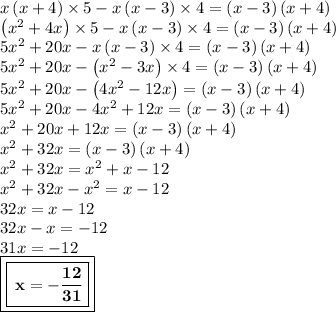
- The value of x is -12/31.
__________________
Hope it'll help you!
ℓu¢αzz ッ