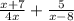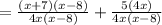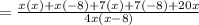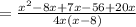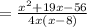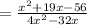Answer:
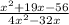
Explanation:
Start by making the denominators of both fraction the same. This can be done by multiplying one fraction's denominator by the other.
After simplifying and combining the two fractions together, check if the numerator can be factorised such that there is a common factor in the denominator and numerator. In this case, the numerator cannot be factorised.
Lastly, expand the denominator.