Answer:
axis of symmetry: x = 2
vertex: (-2, 13)
Explanation:
Given function
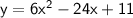
Vertex form
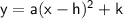
where (h, k) is the vertex
Expand vertex form:
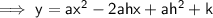
Compare coefficients of expanded vertex form with given function:
coefficient of
 :
:
⇒ a = 6
coefficient of
 :
:
⇒ -2ah = -24
⇒ ah = 12
⇒ 6h = 12
⇒ h = 2
constant:
⇒
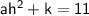
⇒

⇒
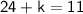
⇒
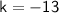
Vertex
Vertex = (2, -13)
Axis of symmetry
Axis of symmetry is when x = h
Therefore, axis of symmetry is x = 2