Answer:
Explanation:

☼︎~Given function is
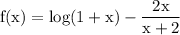
~Let first define the domain of f(x).
![{ \underline { \underline{ {\rule{200cm}{0.4cm}}}}}]()
- Now, log(1 + x) is defined when x + 1 > 0
☼︎~Now, Consider
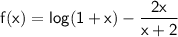
☼︎~On differentiating both sides
w. r. t. x, we get
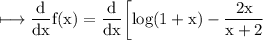
☼︎~We know,
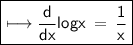
❀And
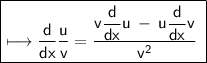
~So, using these results, we get
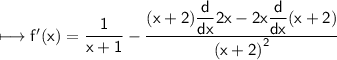
☼︎~We know,
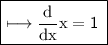
And-
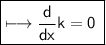
☼︎~So, using this result, we get
![\rm \: f'(x) = (1)/(x + 1) - \frac{(x + 2)2 - 2x(1 + 0)}{ {(x + 2)}^(2) }f′(x)=x+11−(x+2)2(x+2)2−2x(1+0)</strong></p><p><strong>[tex]\rm \: f'(x) = (1)/(x + 1) - \frac{(x + 2)2 - 2x(1 + 0)}{ {(x + 2)}^(2) }f′(x)=x+11−(x+2)2(x+2)2−2x(1+0)\rm \: f'(x) = (1)/(x + 1) - \frac{2x + 4 - 2x}{ {(x + 2)}^(2) }](https://img.qammunity.org/2022/formulas/mathematics/college/a3a3xhstz9z21uatb8rhcx19ggbwxe2cnb.png)
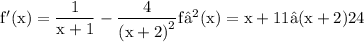
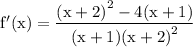
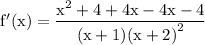
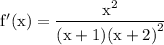
☼︎~Now, as
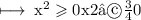
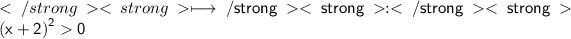
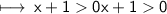
☼︎~So,
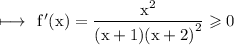
☼︎~Therefore,
- f'(x) is always increasing when x > - 1
![{ \underline { \underline{ \bold {\rule{200cm}{0.4cm}}}}}]()
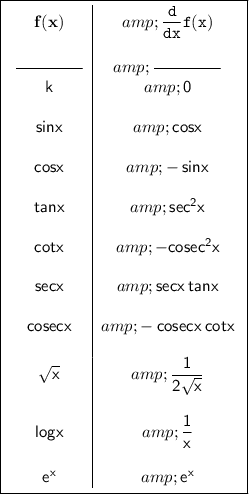
Additional Information:-
![{ \underline { \underline{ \bold {\rule{200cm}{0.3cm}}}}}]()