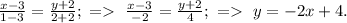1) A(1;2) and slope=3.
slope-interception form is y=s*x+i, where s - slope, i - interception.
if to substitute the given coordinates and slope into the equation, then 2=3*1+i, ⇒ i=-1. It means, the required equation is:
y=3x-1.
2) A(1;2) and B(3;-2).
the common form is:

If to substitute the given coordinates into the common form, then: