Question

Are the graphs of y=3x-5 and 9x+3y=1 parallel, perpendicular or neither?

Answer 1

The two lines are neither parallel nor perpendicular to one another.

Explanation:

The slope
`m` gives the orientation of a line.

Make sure that the equation of both lines are in the slope-intercept form
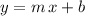`y = m\, x + b` (where
`m\!` is the slope and
`b` is the
`y`-intercept) before comparing their slopes.

The equation of the first line
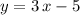`y = 3\, x - 5` is already in the slope-intercept form. Compare this equation with the standard
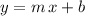`y = m\, x + b`. The slope of this line would be
`m = 3`.

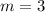Rewrite the equation of the second line
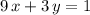`9\, x + 3\, y = 1` to obtain the slope-intercept equation of that line:

`3\, y = -9\, x + 1`.

`\displaystyle y = -3\, x + (1)/(3)`.

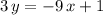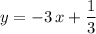Thus, the slope of this line would be
`m = (-3)`.

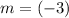Two lines are parallel to one another if and only if their slopes are equal. In this question,
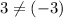`3 \\e (-3)`. Thus, the two lines are not parallel to one another.

On the other hand, two lines are perpendicular to one another if and only if the product of their slopes is
`(-1)`. In this question,
`3* (-3) = (-9)`, which is not
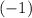`(-1)\!`. Thus, these two lines are not perpendicular to one another, either.