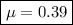Question

PHYSICS 1403

Lab Homework - Friction on a Ramp
A laborer wants to move crates containing bottles of olive oil from a truck to the ground by sliding them
along a ramp. The ramp is 6 m long and is at an angle of 25º. There is friction on the ramp for the first
crate. The laborer doesn't know that there is a small leak in one of the bottles. The leak leaves a layer of
oil on the ramp. The oil creates a frictionless surface for the second crate Wayne sends down the ramp. At the bottom of the ramp, the speed of the second crate (without friction) is 2.5 the speed of the first crate (with friction). Find the coefficient of kinetic friction. Hint: this is a multistep problem that is
be solved using only energy equations. Do not use kinematics or you will not receive full
credit, even if your answer is correct. Use conservation of energy and start with the frictionless case.

Answer 1

Hi there!

Hi there!

We can begin by simplifying the work-energy theorem for Crate 2.

Since there is no friction, there is no energy dissipated. Thus, the initial energy is equal to the final energy.

Initially, we only have gravitational potential energy (U = mgh), and when the box has fully slid down, it only has kinetic energy (KE = 1/2mv²), therefore:

`E_i = E_f\\\\mgh = (1)/(2)mv^2`

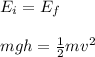
We can cancel out the mass and solve for velocity.

`gh = (1)/(2)v^2\\\\v^2 = 2gh \\\\v = √(2gh)`

We must use right triangle trigonometry to solve for the HEIGHT given the ramp's length (hypotenuse).

We can use sine:

`sin\theta = \frac{\text{h}}{L} \\\\Lsin\theta = h = 6 * sin(25) = 2.5357 m`

Now, solve for velocity.

`v = √(2(9.8)(2.5357)) = 7.05 (m)/(s)`

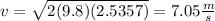
Since this is 2.5 times the speed of the first crate, we know that the final velocity of crate 1 is:

`v_1 = (v)/(2.5) = 2.82 (m)/(s)`

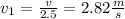
Crate 1:
In this instance, we have friction. Recall the following.

`F_f = \mu N`

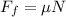
On an incline, the normal force is equivalent to the cosine of the force of gravity, so:

`N = mgcos\theta`

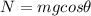
Now, create an equation for the force due to friction.

`F_f = \mu mgcos\theta`

The work done by any force is:

`W = F \cdot d\\\\W_f = \mu mgdcos\theta`

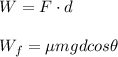
In this instance, d = the ramp's length, or 6 m.

Now, we can use the work-energy theorem.

Ei = Ef

However, there is energy dissipated; we can call this Wf (Work due to friction). Therefore:
Ei - Wf = Ef

Now, we can rearrange to solve for Wf:
Ei - Ef = Wf

Like above, there is initially only GPE (U = mgh) and finally only KE (K = 1/2mv²), so:

`mgh - (1)/(2)mv^2 = \mu mgdcos\theta`

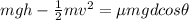
Solve for the coefficient of friction. Begin by canceling out the mass and multiplying all terms by 2:

`2mgh - mv^2 = 2\mu mgdcos\theta\\\\2gh - v^2 = 2\mu gdcos\theta\\\\\mu = (2gh - v^2)/(2gdcos\theta)\\\\\mu = (2(9.8)( 2.5357)- (2.82)^2)/(2(9.8)(6)cos(25))`

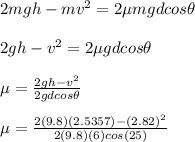
Evaluate:

`\boxed{\mu = 0.39}`