Answer:
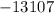
Explanation:
We would like to evaluate the following Geometric Series ,
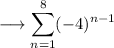
In a geometric series, a common number is multiplied to the previous term in order to find the next term . And that common number is called common ratio (r) .
As we know that ,
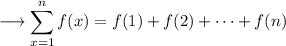
So , we can write the series as ,
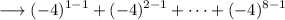
Simplify,
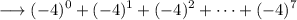
We can find the common ratio by dividing and successive term by its preceding term , as ;

Again , here ;
- First term = a =
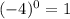
- Common ratio =
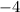
- number of terms (n) = 8
And we can find the sum of geometric series using the formula , ( this is used when the value of r is less than 1 , here it is -4 ) .
![\displaystyle\longrightarrow \Bigg[ Sum = (a(1-r^n))/(1-r)\Bigg]](https://img.qammunity.org/2023/formulas/mathematics/high-school/b03as9d1wmo8mvp6hjwmbu0e9al46937nw.png)
- where the symbols have their usual meaning.
On substituting the respective values, we have;
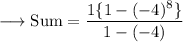
Simplify ,
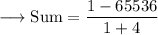
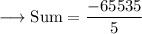
Simplify by dividing ,
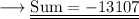
And we are done !