Answer:
t = 40
Explanation:
Given the logarithmic expression:
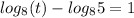
Use the Logarithmic Property (Quotient Rule):
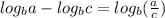
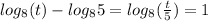
Next, using the Logarithmic Property:
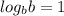
We must determine the possible value of t that can be divided by 5 to produce a quotient of 8 that will make the logarithmic property,
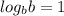 , true. In that case, t = 40 divided by 5 results in a quotient of 8.
, true. In that case, t = 40 divided by 5 results in a quotient of 8.
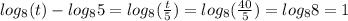
Therefore, the value of t = 40.